A 29.
- EGYBEN ELSÕ NEMZETKÖZI -
ORTVAY RUDOLF
FIZIKAI PROBLÉMAMEGOLDÓ VERSENY
FELADATAI
1998
Az ELTE TTK Fizikus Diákköre és a Magyar Fizikus Hallgatók Egyesülete
1998-ban is meghirdeti a hagyományos,
immár 29-ik, ezúttal elsõ ízben nemzetközi Ortvay Rudolf Fizikai
Feladatmegoldó Versenyt.
Idõpont: 1998. október 30 - november 9.
Az Ortvay verseny régi hagyomány az Eötvös Loránd Tudományegyetemen.
A hajdani versenyzõk közül sokan már híres
tudósok, egyetemi professzorok - annak idején az Ortvay-feladatok
megoldása során mutatták meg oroszlánkörmeiket.
A verseny 1998-ban elõször - de reméljük, nem utoljára -
nemzetközi lesz.
Elõzetes propagandánk hatására máris több
mint húsz országból érkeztek érdeklõdõ levelek. Igy alkalom adódik arra,
hogy a különbözõ országok és különbözõ
egyetemek hallgatói összémérhessék tudásukat, ötleteiket, feladatmegoldó
képességüket és a rutinon túlmutató, a feladatok
mélyére hatoló fizikai érzéküket. Bár a díjazás egyéni, egy ilyen széles
körû verseny egyben az anyaintézmények, a
versenyzõk tudását és képességeit csiszoló egyetemek vetélkedése is.
Az Ortvay versenyen minden egyetemi hallgató indulhat - az értékelés és
a díjazás évfolyamonként történik. A doktoranduszok külön kategóriát
alkotnak. A verseny egyéni: páros vagy csoportosan írt dolgozatokat nem
fogadunk el. Kérjük megadni a versenyzõ egyetemét, szakát és évfolyamát.
Álnév vagy jelszó nem használható, minden versenyzõ valódi néven indul.
A feladatok 1998. október 30-án, pénteken, közép-európai idõ szerint 12
órától magyar és angol nyelven, html és LATEX
formátumban letölthetõk az Ortvay-verseny weblapjáról
http://ludens.elte.hu/ortvay.
A dgy@ludens.elte.hu
e-mail címre megküldött elõzetes kérésre e-mailen is postázzuk a feladatokat.
Budapesten emellett a feladatok - ugyanettõl az
idõponttól - nyomtatott formában is átvehetõk a Gólyavárban
(H-1088 Budapest, Múzeum krt. 6-8.) és az ELTE Lágymányosi Fizika-Kémia
tömbjének (H-1117 Budapest, Pázmány Péter sétány 1/A)
földszinti társalgójában. A Gólyavárban, a Hallgatói Irodában a késõbbiekben
egy mesterpéldány áll a fénymásolni kivánók rendelkezésére.
A BME-n, a JATE-n, a KLTE-n és számos külföldi egyetemen helyi szervezõk
intézik a feladatok sokszorosítását és kiosztását.
Figyelem! A szervezõk minden igyekezete ellenére is elõfordulhat, hogy
egy-egy értelemzavaró fogalmazási vagy gépelési hiba marad a feladatok
szövegében. Érdemes ezért a továbbiakban is figyelni a fenti weblapot,
illetve a gólyavári és
lágymányosi hirdetõtáblát, ahol az esetleges javításokat, módosításokat
azonnal közzétesszük.
A verseny feladatai az elméleti fizika különbözõ területeirõl és a
fizika alkalmazásai körébõl származnak. Egy évben általában
30 - 35 feladatot tûzünk ki. Ezek különbözõ nehézségi fokúak, de minden
hallgató találhat évfolyamának megfelelõ feladatokat. Egy versenyzõ
maximálisan 10 feladat megoldását adhatja be. Minden feladat megoldására
maximálisan 100 pontot lehet kapni.
A feladatok megoldásához
bármilyen segédeszköz használható. Könyvre, folyóiratcikkre hivatkozni
lehet.
Minden feladat megoldását külön A4-es lap(ok)ra kérjük
leírni.
Egy lapnak csak az egyik oldalára írjunk vagy nyomtassunk! Ne
írjunk
ceruzával vagy vékony másolópapírra - ezeket nem tudjuk
elfaxolni a
megoldások javítóinak. Az ilyen dolgozatokat nem fogadjuk el.
Ha a megoldáshoz számítógépes program is tartozik, kérjük írásban megadni a
program részletes dokumentációját (milyen nyelven írodott, hogyan lehet
elindítani, milyen paramétereket lehet beállítani, melyik betû mit
jelent, hogyan kell a program készítette ábrákat vagy táblázatokat
értelmezni, stb.) A programokat floppylemezen lehet
mellékelni, vagy e-mailen lehet elküldeni az alább megadott címre.
A megoldásokat személyesen, postán, faxon vagy e-mailen
(LATEX formátumban, vagy, ha
nincsenek benne képletek, közönséges elektronikus levélben) lehet
beküldeni.
Személyesen a HALI-1-ben vagy a Lágymányosi Északi több
földszintjén
Postacím: Fizikus Diákkör, Dávid Gyula,
ELTE TTK Hallgatói Iroda, Gólyavár,
H-1088 Budapest, Múzeum krt. 6-8.
Faxszám: Dávid Gyula, 36/1/2662556
E-mail cím: dgy@ludens.elte.hu.
Beadási határidõ: november 9. hétfõ, közép-európai idõ szerint 12 óra.
A verseny díjazása évfolyamonként történik, az összpontszám alapján.
A zsüri fenntartja a jogot, hogy egyes díjakat ne, megosztva vagy
több példányban adjon ki. A pénzjutalommal járó elsõ, második és harmadik
díjak mellett dicséretek, illetve egyes feladatok kivaló megoldásáért
különdíjak is odaítélhetõk. Ezért már egy-két
feladat megoldását is érdemes
beadni!
A verseny hagyományos szponzorai az ELTE TTK Hallgatói Alapítványa és az
Eötvös Loránd Fizikai Társulat.
Emellett idén régi mecénásunk, Diósi Lajos 20 000 Ft különdíjat ajánlott fel.
A legjobb eredményt elérõ szegedi versenyzõt
a Pro Physica Hallgatói Alapítvány 5000 Ft különdíjjal jutalmazza.
Köszönjük az eddigi támogatásokat - és köszönettel fogadjuk a
továbbiakat is.
A verseny eredményhirdetése december 10-én lesz, a hagyományos
Fizikus Mikulással egybekötve. A pontos helyszínt
késõbb közöljük a verseny weblapján. Az ünnepélyes eredményhirdetést a
feladatok megoldásának megvitatása követi. Az egyes feladatok legjobb
megoldóit ezennel elõre felkérjük, hogy ismertessék megoldásaikat.
(A verseny egész Földre kiterjedt volta ellenére ez a felkérés
értelemszerûen csak a hazai versenyzõkre vonatkozik.) A részletes
eredmény ezután megtekinthetõ lesz a
verseny weblapján. A díjazott versenyzõket e-mailben értesítjük, az
okleveleket és a pénzjutalmakat postán küldjük el.
A verseny feladatait és megoldásaikat - az egyes feladatok legjobb
megoldóinak szövegezésében (melyre õket ezennel felkérjük) -
angol nyelvû kiadványban szeretnénk megjelentetni. Ezt a kiadványt a
fizikushallgatók nemzetközi szervezete, az IAPS, valamint a verseny résztvevõi
segítségével világszerte terjeszteni kívánjuk. Reméljük, ez még jobban
hozzájárul a verseny nemzetközivé válásához.
Sikeres versenyzést, tartalmas és hasznos fejtörést kívánunk minden
versenyzõnek!
A verseny szervezõi nevében
Dávid Gyula
ELTE TTK Fizikus Diákkör
dgy@ludens.elte.hu
- 1.
- A bor erjedéssel készül a szõlõbõl. Ennek
során hõ keletkezik.
a) Hány fokosra melegszik fel egy 500 literes
hordó a különféle borfajták esetén?
b) Melyek a legfontosabb
paraméterek, amik meghatározzák ezt a hõmérsékletet?
c) Az erjesztõ baktériumok egy bizonyos hõmérséklet felett
elpusztulnak. Legfeljebb mekkora méretû lehet az a hordó, amiben
mindenütt forrásban marad a must? Hogyan függ ez a méret a
külsõ hõmérséklettõl?
(Horváth Anna)
- 2.
- Ha két párhuzamosan állított tükör közé nézünk,
képek végtelennnek tûnõ sorozatát látjuk. A tükör
véges mérete miatt azonban csak véges számú kép látható.
a) Hogyan függ a látható képek száma a tükör
méretétõl, alakjától?
b) Vizsgáljunk több különféle módszert, amivel a párhuzamos
tükrökben látható képeket megfigyelhetjük! (Csak
kísérletileg megvalósítható eseteket diszkutáljunk!)
(Horváth Anna)
- 3.
- Téli reggeleken az autók ablaka sokszor csak a Nap felõli
oldalon van befagyva.
Miért? Adjunk kvantitatív magyarázatot!
(Bene Gyula)
- 4.
- A feladat szövege
2 mondattal bõvült
Egy faltól a távolságban elhelyezett csuklós talpon
rögzítjük egy l > a hosszúságú seprûnyél
alsó végét.
A nyél felsõ vége a falnak támaszkodik. Döntsük
most kissé oldalt a seprûnyelet: a súrlódás
következtében egy ideig még egyensúlyban maradhat.
Mekkora az a kritikus szög, amelynél már megcsúszik
a seprûnyél?
(Gnädig Péter)
- 5.
- Adott méretû,
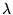 és
és 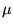 rugalmassági állandókkal
jellemezhetõ téglákból tornyot építünk.
Milyen magas torony áll még stabilan?
rugalmassági állandókkal
jellemezhetõ téglákból tornyot építünk.
Milyen magas torony áll még stabilan?
(Tichy Géza)
- 6.
- Rugalmasságtanban az ui elmozdulásvektorból származtatott
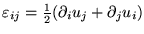 deformációs tenzorra
érvényes az alábbi kompatibilítási feltétel (a
képletben
deformációs tenzorra
érvényes az alábbi kompatibilítási feltétel (a
képletben
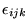 a Levi-Civita-féle teljesen antiszimmetrikus
egységtenzort jelöli):
a Levi-Civita-féle teljesen antiszimmetrikus
egységtenzort jelöli):
Állítsuk elõ a deformációs tenzorból az elmozdulásvektort!
(Tichy Géza)
- 7.
- A hallás finomságát meghatározó egyik mechanikai tényezõ
a dobhártya alakja. Magyarázzuk meg, miért alkalmasabb a
szabályos alakú (kör, ellipszis) dobhártya a finom hallásra, mint a
szabálytalan! (Megjegyzés: a hallás finomságán azt értjük, hogy mennyire
képes valaki megkülönböztetni két, egymáshoz közeli frekvenciájú hangot).
(Horváth Anna)
- 8.
- Az emberi vér nem képes arra, hogy fizikailag oldott
állapotban elegendõ mennyiségû oxigént szállítson.
Ezért is vannak
vörösvértestjeink (VVT), melyek ezt a feladatot el tudják végezni.
De vajon mennyibe is "kerülhet" ez nekünk?
Mennyi plusz energiát fordít a VVT-k
szállítására egy átlagos napján egy átlagos ember
ahhoz a hipotetikus esethez képest, amikor - ugyanakkora
össztérfogatú vér mellett -
nem lenne szüksége
VVT-kre?
Néhány figyelembe veendõ szempont: a VVT-ket át kell tuszkolni a
kapillárisokon (hiszen azok átmérõje kisebb, mint a VVT-ké);
a vér gyorsabban
áramlik, mint a VVT-k; a VVT és a vér sûrûsége eltérõ,
így a nehézségi erõ
miatt többletenergia szükséges a VVT mozgatásához.
(Nagy György)
- 9.
- Egy kirándulás alkalmával elkapott minket az esõ. Egy
útbaesõ pince
eresze alól nézegettük a reménytelen idõt és az eresz alján
össze-összegyülõ vízcseppeket, amelyek növekedvén
elindultak az eresz
alján a lefolyó felé, de útközben meghízva lecsöppentek.
Vizsgáljuk meg a
csepp kialakulásához vezetõ instabilitást! Adjuk meg a csepp
hely-idõ függvényét a
lecsöppenés helyéig! Utolérhet-e egy csepp egy másikat?
(Török János)
- 10.
- Egy pipettát tartunk függõlegesen, szájával lefelé.
A pipettából folyadék áramlik ki állandó sebességgel.
Milyen feltételek mellett
alakulnak ki cseppek a pipetta szájánál?
Ha teljesülnek ezek a feltételek, akkor határozzuk meg
a cseppek alakját az idõ függvényében!
(Zénó Farkas)
- 11.
- Ha függõleges (üveg)csõbe száraz homokot töltünk, a lefelé áramló
anyagban sûrûséghullámok indulnak el fölfelé. (Érdemes kipróbálni!)
A jelenség hasonlít a közlekedési torlódások terjedéséhez.
Mi a magyarázata? Mitõl függ a hullámok sebessége?
(Kertész János)
- 12.
- L. Niven Gyûrûvilág címû fantasztikus
regényében - egyéb érdekes technikai ötletek
mellett - említés történik a következõ szerkezetrõl is:
egy csillag körüli kör mentén
egyenletes térközökben körpályára állítanak igen nagy
számú egyforma
mesterséges bolygót. Az objektumokat a kör mentén nyújthatatlan
lánccal
kötik össze, majd a rendszert rakétákkal felpörgetik az adott
sugárhoz tartozó orbitális
szögsebesség többszörösére. (Hogy mire jó ez az egész,
az kiderül a regénybõl.)
Vizsgáljuk meg a rendszer stabilitását, és határozzuk meg a
kör mentén terjedõ hullámok
diszperziós relációját longitudinális, radiális, illetve a
pálya síkjára merõleges
perturbációk esetén!
(Dávid Gyula)
- 13.
- Két egyforma szigetelõ korongot azonos mennyiségû
pozitív töltéssel látunk el. Közelítsük egymáshoz
a két párhuzamos korongot! Mekkora erõ kell ehhez?
Vázoljuk fel a két korong között kialakuló elektromos
teret!
(Radnai Gyula - Gnädig Péter)
- 14.
- Milyen alakúra hajlítsunk össze egy adott szigetelt
rézhuzalt, hogy a lehetõ legnagyobb legyen az induktívitása?
Legyen az l= 5 m hosszú homogén rézhuzal keresztmetszete r= 0,4 mm
sugarú kör, a rajta lévõ szigetelõ réteg vastagsága
s= 0,1 mm. Mekkora
lesz ennek a szigetelt huzalnak a maximális induktívitása?
(Ferromágneses anyag nincs a közelben.)
Bemelegítésül határozzuk meg e huzalból hajlított kör,
illetve négyzet alakú hurok induktívitásának arányát!
(Radnai Gyula)
- 15.
- Tegyük fel, hogy az elektromágneses négyespotenciál (Ai) és a
negyesáram-sûrûség (ji) komponensei nem valós, hanem a) komplex;
b) kvaternió értékeket vehetnek fel!
Konstruáljuk meg a Lorentz-invariáns valós hatásintegrált, és vezessük le
a téregyenleteket!
"Fordítsuk le" a hiper-Maxwell-egyenleteket valós hármasvektor-mezõkre
felírt parciális differenciálegyenlet-rendszerre, és keressünk meg néhány
érdekes megoldást (ötletek: síkhullám, monopólus, Green-függvény)!
Milyen új, a szokásos elméletben nem szereplõ szimmetriái vannak az új
elméletnek? Melyek a megfelelõ megmaradási tételek?
Milyen valóságos jelenségek modellezésére lehetne felhasználni ezt a
(hiper)komplex elektrodinamikát?
Egeszítsük ki a hatásintegrált tömegtaggal is, és vizsgáljuk meg ennek
következményeit!
(Dávid Gyula)
- 16.
- Az elsõ, és egyben utolsó Forma-42 fotonrakéta-versenyt 2442-ben
rendezték meg a
vadregényes Minkowski-téren, mindjárt a Tejút legszélsõ
spirálkarjain túl, kint a nagy
semmiben. Itt kellett tartani a versenyt, mert az ÛrKRESZ meglehetõsen
szigorú:
rendelkezései szerint a fotonrakéták semmilyen körülmények
között sem közelíthetik
meg egymást 1000 km-nél jobban. Szükség volt tehát a helyre!
A Forma-42
versenyen részt vevõ rakéták 1 km hosszú, 10 m átmérõjû
forgásellipszoidok. (A
hatalmas test 42 évnyi szakadatlan üzemre elegendõ anamezont, az
antianyagnál is
hatékonyabb üzemanyagot rejt magában.) Az orrukon és tatjukon
elhelyezett
pozíciójelzõ lámpák a Hajózási Szabályzatnak
megfelelõen másodpercenként
bocsátanak ki egy zöld, illetve vörös fényjelet. Bernie Ecclestar,
a fõszervezõ a
sportszerûség érdekében úgy rendelkezett, hogy valamennyi
versenyzõ ûrhajóját
egyforma hajtómûvel szereljék fel (de ezt persze nem kötötték a
közönség orrára). Ez a "Mintha otthon lennél"
típusú fotonmotor
pontosan 1 g-nyi sajátgyorsulást szolgáltat az ûrhajónak,
így a pilóta valóban úgy érzi
magát, mintha otthon ülne (a játékteremben). Sajnálatos mûszaki
hibák miatt a 42
indulóból negyvennek vissza kellett lépnie. A megmaradt két rakéta
versenye kissé
unalmasra sikeredett: mintegy százezer km távolságban egymás mellett
lebegve
egyszerre indultak el a startvonalra merõleges irányba, aztán -
lévén tökéletesen
egyforma szerkezetûek - egymással párhuzamosan, végig egyenes
vonalban és
azonos gyorsulással futva, a tökéletes szimmetria jegyében
döntetlen eredményt
értek el. A nézõközönség persze nem sokat látott az
elszáguldó rakétákból - még
szerencse, hogy a konkurrens tv-társaságok kamerákat és
robottudósítókat
helyeztek el az egyik, illetve másik rakéta fedélzetén. Az
automata kamerák a másik
versenyzõ rakétára irányultak - mi mást is nézhettek volna?
-, a robotriporterek pedig
izgatottan követték a kamera tartószerkezetének akármilyen
csekély elfordulását is,
mert ebbõl (meg persze a másik rakéta látszó
szögátmérõjének és orientációjának
változásából) próbáltak következtetni a verseny pillanatnyi
állására. Így aztán elég
izgalmas virtuális verseny kerekedett ki a tv-képernyökön. Amikor
aztán a második
futam során az egyik rakéta a startnál udvariasan százezer km
elõnyt adott a
másiknak, és így pontosan egyszerre indulva, pontosan egymás
nyomában futották
végig a nyílegyenes kozmikus pályát, a két ûrhajó
fedélzetén tartózkodó
robotriporterek valóságos extázisba esve közvetítették a
kameráik által látott,
meglehetõsen furcsa versenyt.
Számítsuk ki/írjuk le/rajzoljuk le, mit láttak a kamerák az
elsõ futam alatt, majd a
második futamban az elöl, illetve a hátul haladó ûrhajóból
nézve! Hogy változott a
másik rakéta távolsága, iránya, orientációja, szögmérete,
jelzõfényeinek színe,
fényessége? Pótkérdés: hogyan, mikor és miért ért véget
a verseny?
(Dávid Gyula)
- 17.
- A Forma-42 versenyen részt vevõ két rakéta pilótái
elhatározzák, hogy megvizsgálják
Einstein híres régi paradoxonját a (kilo)méterrudak
rövidülésérõl. Ezért a két, egymás
mögött lebegõ ûrhajót összekötik egy 1 km hosszú rúddal.
Egy elõre rögzített
pillanatban egyszerre bekapcsolják mindkét rakéta hajtómûvét,
majd 1 másodpercnyi
mûködés után kikapcsolják. (A gyorsítás iránya a
rúd által meghatározott
egyenesbe esik.) A pilóták jártak a tudományos óvódába,
ezért tudják, hogy a
relativitáselmélet szerint merev test nem létezik, és a két
végét ért erõhatás
következtében a rúdban longitudinális rugalmas hullámok keletkeznek.
Ezt
figyelembe veendõ már jó elõre megvizsgálták a rúd
rugalmas tulajdonságait, és
megmérték a csillapodó longitudinális hullámokra vonatkozó
telegráfegyenlet együtthatóit. Ezért
bíznak benne, hogy a hullámok szép lassan lecsillapodnak, és a
rúd végül nyugalmi
állapotba kerül a két rakéta új inerciarendszerében.
Kövessük a hullámok terjedését
a gyorsítás szakaszában, illetve a hajtómûvek kikapcsolása
után, és határozzuk meg
a rúd hosszát a végállapotban! Mit szól ehhez Einstein professzor?
(Dávid Gyula)
- 18.
- A Forma-42 versenyen részt vett fotonrakéták egyike ezúttal
(még bõségesebb,
gyakorlatilag korlátlan üzemanyagkészlettel feltöltve) a még a
Minkowski-térnél is
vadregényesebb Riemann-téren indul próbaútra. A Naprendszer szélén
lebegve
megcélozza az éggömb egyik sötét, galaxisoktól mentes pontját,
aztán hegyibe!
Útközben persze a személyzet érdeklõdéssel figyeli a
Világegyetem érdekes
tájait. Mit látnak az
ûrhajósok az út során? Hogyan változik a galaxisok
fényessége, eloszlása, a kozmikus
háttérsugárzás szögeloszlása és hõmérséklete az
irány függvényében? A kért
adatokat az ûrhajó sajátidejében mérve számítsuk ki és
ábrázoljuk! Adjuk meg a
választ az Einstein-féle sztatikus, valamint a Fridman-féle zárt,
nyílt, illetve
euklideszi terû táguló Világegyetem esetén is! Mi lesz az
ûrhajó sorsa a távoli
jövõben?
(Dávid Gyula)
- 19.
- Egyesek szerint a 2+1 dimenziós általános
relativitáselméletben a kozmikus
objektumok között nincs gravitációs kölcsönhatás.
(Miért, a 3+1 dimenziós
elméletben van?) Ha a fenti állítás igaz, akkor mi a csudáról
szól egyáltalán a 2+1
dimenziós elmélet? Ha pedig nem igaz az állítás, akkor
miért igaz mégis?
(Dávid Gyula)
- 20.
- Határozzuk meg a következõ Hamilton-operátor sajátértékeit
(József Cserti)
- 21.
- A spin mellett talán a határozatlansági reláció,
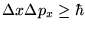 ,
stb. az, amire a legtöbbször utalnak
úgy, hogy "tisztán kvantummechanikai jelenség, amelynek
nincs klasszikus megfelelõje".
A szárnyaló elméknek azonban ez ködösítésnek tûnhet, és felmerülhet az
axiomatikus kvantummechanika eme bástyája ellen intézendõ támadás
szükségessége. Talán nem is állnak olyan rosszul a dolgok, és a
kvantum-klasszikus korrespondenciára éhezõ szépérzékünk végsõ soron
nem sérül.
A határozatlansági relációban egy tetszõleges A fizikai mennyiség
átlagértéke körüli szórását kell kiszámítani:
,
stb. az, amire a legtöbbször utalnak
úgy, hogy "tisztán kvantummechanikai jelenség, amelynek
nincs klasszikus megfelelõje".
A szárnyaló elméknek azonban ez ködösítésnek tûnhet, és felmerülhet az
axiomatikus kvantummechanika eme bástyája ellen intézendõ támadás
szükségessége. Talán nem is állnak olyan rosszul a dolgok, és a
kvantum-klasszikus korrespondenciára éhezõ szépérzékünk végsõ soron
nem sérül.
A határozatlansági relációban egy tetszõleges A fizikai mennyiség
átlagértéke körüli szórását kell kiszámítani:
A kvantummechanika (QM) keretein belül a fent használt átlag (az
egyszerûség kedvéért az egydimenziós esetben) a következõ integrált jelenti:
ahol 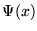 rendszer normált hullámfüggvénye.
A klasszikus mechanikában (CM) persze már bajosabb megadni azt, hogy mit
érthetnénk ezen az átlagon, de munkahipotézisként
- jobb híján - értelmezzük A átlagát az
rendszer normált hullámfüggvénye.
A klasszikus mechanikában (CM) persze már bajosabb megadni azt, hogy mit
érthetnénk ezen az átlagon, de munkahipotézisként
- jobb híján - értelmezzük A átlagát az
idõátlaggal, aztán nézzük meg, hogy ezzel mire jutunk.
Ahhoz, hogy ellenõrizhessük ennek a némileg merész választásnak a
létjogosultságát, tekintsünk egy konkrét rendszert.
Az
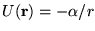 vonzó centrális potenciálban történõ
klasszikus mozgás (Kepler-probléma) és kvantumos mozgás (hidrogénatom)
közti hasonlóságokra (pl. szimmetriák) már régen felfigyeltek;
a részletek (pályák, hullámfüggvények, energiák, stb.) pedig jól ismertek.
vonzó centrális potenciálban történõ
klasszikus mozgás (Kepler-probléma) és kvantumos mozgás (hidrogénatom)
közti hasonlóságokra (pl. szimmetriák) már régen felfigyeltek;
a részletek (pályák, hullámfüggvények, energiák, stb.) pedig jól ismertek.
Keressük meg a megfelelõ koordinátákat és változókat, majd
számítsuk ki a szórásokat egy alkalmasan választott koordinátára és a
hozzátartozó impulzusra nézve! Használjuk a fenti definíciókat
(ha tudunk
jobbat ajánlani, akkor hajrá...)! Van-e kapcsolat a klasszikus és a
kvantummechanikai eredmények között?
Lehet-e ezek alapján klasszikus határozatlansági relációról
beszélni? Mit jelent itt az átlag klasszikus definíciója?
(Magyar Péter)
- 22.
Tekintsük a
Hamilton-függvény által definiált rendszert, ahol
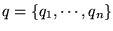 az általános koordináták összességét jelöli.
Kvantáljuk a rendszert a
az általános koordináták összességét jelöli.
Kvantáljuk a rendszert a
Schrödinger-féle elõírás szerint. Az operátorok
sorrendjének határozatlanságát a
skalárszorzat szerinti önadjungáltság megkövetelésével
szüntetjük meg.
Hogyan kell transzformálni a hullámfüggvényeket a
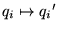 általános koordinátatranszformáció során, ha azt akarjuk,
hogy
általános koordinátatranszformáció során, ha azt akarjuk,
hogy 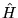 kovariánsan transzformálódjon?
Alkalmazzuk a fenti eredményeket a kétdimenziós harmonikus
oszcillátorra Descartes- és polárkoordináta-rendszer-beli
kvantálás esetén!
kovariánsan transzformálódjon?
Alkalmazzuk a fenti eredményeket a kétdimenziós harmonikus
oszcillátorra Descartes- és polárkoordináta-rendszer-beli
kvantálás esetén!
(Bajnok Zoltán)
- 23.
- Az elektronok fermionok, így a Pauli-elv értelmében nem kerülhetnek
azonos állapotba. A szupravezetõkben az elektronok
párokba állnak össze (Cooper-párok), amelyek bozonok, és így
azonos állapotba is kerülhetnek. Nincs itt ellentmondás? Indokoljuk
a választ számítással!
(Bene Gyula)
- 24.
- Vizsgáljuk meg, lehet-e koherens állapotokat értelmezni
síkrotátor
esetében! A harmonikus oszcillátor koherens állapotainak mely
tulajdonságait lehet átmenteni, illetve mirõl kell lemondani? Mi
az új koherens állapotok
kapcsolata a léptetõ operátorokkal?
(Borsányi Szabolcs)
- 25.
- Két bozon mozog egydimenziós, végtelen mély potenciálvölgyben
(azaz V(x)=0, ha
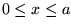 és
és
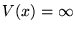 egyébként).
Egymással merev gömbként ütköznek. Határozzuk meg az
energia-sajátértékeket és az energia-sajátfüggvényeket!
egyébként).
Egymással merev gömbként ütköznek. Határozzuk meg az
energia-sajátértékeket és az energia-sajátfüggvényeket!
(Bene Gyula)
- 26.
- A csapdába zárt, Bose-kondenzálódó alkáli-atomok
alacsony energiás gerjesztéseit a következõ
sajátérték-probléma megoldása adja meg:
A kísérletekben az
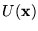 potenciál
potenciál
alakú, ahol 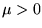 a kémiai potenciál, m az alkáliatomok
tömege,
a kémiai potenciál, m az alkáliatomok
tömege, 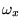 ,
,
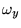 ,
,
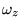 a csapda jellemzõi,
a csapda jellemzõi,
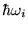 pedig a gerjesztések energiái.
Milyen további, az x, y, z koordinátákat, illetve az azok szerinti
deriváltakat tartalmazó, operátorok felcserélhetõk
pedig a gerjesztések energiái.
Milyen további, az x, y, z koordinátákat, illetve az azok szerinti
deriváltakat tartalmazó, operátorok felcserélhetõk 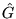 -vel?
-vel?
(Csordás András)
- 27.
- Fenntartható-e egy egyatomos ideális gázban ütközések nélkül,
pusztán csak
a részecskék szabad áramlásával a lokális egyensúly? A válasz erre a
kérdésre meglepõ módon igen. Miért? Adjuk meg a
fázistér
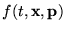 eloszlásfüggvényének, az
eloszlásfüggvényének, az
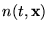 lokális sûrûségnek, a
lokális sûrûségnek, a
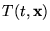 hõmérséklettérnek és a
hõmérséklettérnek és a
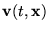 sebességtérnek az idõfüggését egy ilyen ütközésmentes,
lokálisan termalizált gázra!
sebességtérnek az idõfüggését egy ilyen ütközésmentes,
lokálisan termalizált gázra!
(Csörgõ Tamás)
- 28.
- A termionok - mint az 1996. évi Ortvay verseny óta tudjuk -
olyan (hipotetikus) részecskék, amelyek igen gyorsan felveszik a
környezet
hõmérsékletét. Boltzmann szerint E=kT, Einstein szerint
E=mc2, szóval
a termionok tömege mindig arányos a környezet lokális
hõmérsékletével.
Ezt nem kell bebizonyítani, ezt egyszerûen el kell hinni.
A termionoknak három fajtája van. A forronok szeretik a meleget,
ezért
rájuk a hõmérséklet gradiensével arányos erõ hat. A
vacogonok
ezzel szemben hidegkedvelõk, ezért a rájuk ható erõ az elõbbivel
ellentétes irányú, bár nagyságra megegyezõ. A temperonok
a szelid,
langyos vidéket kedvelik, ezért rájuk a sebességük és a
hõmérséklet-gradiens
vektoriális szorzatával arányos erõ hat. (A számolás során
az igényeknek megfelelõen további altípusokat is definiálhatunk.)
Tanács: a fellépõ sebességdimenziójú
állandókat célszerû
c-vel jelölni.
Vizsgáljuk meg a termionok egyik vagy másik fajtájából álló ideális gáz
termodinamikáját! Vezzesük le a megfelelõ állapotegyenleteket!
Mi történik ha egy mozgó dugattyúval - a) eset: a dugattyú
hõszigetelõ; b) eset: a dugattyú hõvezetõ - elválasztott
henger két része két
különbözõ termionfajtából álló gázt tartalmaz?
Mi történik, ha megengedjük a kétféle gáz keveredését?
Vizsgáljuk meg a rendszer mechanikai és termodinamikai stabilitását!
(Dávid Gyula)
- 29.
- Az átlagtér-közelítés az Ising-modell megoldását egyetlen spin
vizsgálatára egyszerûsíti: egy kiválasztott spint egzaktul tárgyalunk,
miközben a kölcsönható szomszédokat átlagértékükkel helyettesítjük. Az a
tény, hogy az Ising-lánc egzaktul megoldható, a közelítés kiterjesztését
sugallja: a modellt kölcsönható láncok rendszerének tekintve, egy
kiválasztott láncot egzaktul tárgyalunk, miközben a szomszédos láncok
spinjeit átlagértékükkel helyettesítjük.
A két közelítés összehasonlítására számítsuk ki mindkét módon annak az
Ising-modellnek az átalakulási hõmérsékletét, amelyben a spinek egy
egyszerû köbös rács pontjaiban helyezkednek el, és a kicserélõdési
együtthatók különbözõ értékeket vesznek fel az xy síkban és a z
tengely irányában. A modell energiája
ahol az i,j,k egész számok a rácspontok koordinátái, és
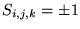 .
.
(Sasvári László)
- 30.
- Tekintsünk egy egydimenziós láncot, amelynek mentén egymástól szabályos
a távolságra egyforma
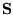 (
(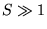 )
spinek
helyezkednek el. A spinek (az elektronfelhõ alakjában megnyilvánuló atomi
szimmetriák miatt) csak az x-y síkban tudnak forogni, azaz a lánc
tengelyére
(z-tengely) merõlegesen, a kialakuló struktúra pedig (T=0
hõmérsékleten, külsõ tér nélkül) egy (két szomszédos pont között)
)
spinek
helyezkednek el. A spinek (az elektronfelhõ alakjában megnyilvánuló atomi
szimmetriák miatt) csak az x-y síkban tudnak forogni, azaz a lánc
tengelyére
(z-tengely) merõlegesen, a kialakuló struktúra pedig (T=0
hõmérsékleten, külsõ tér nélkül) egy (két szomszédos pont között)
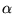 szöggel elforduló spirál.
Ez a modell helyesen írja le egyes ritkaföldfémek és átmenetifém-vegyületek
alapállapotát, amelyekben ismereteink szerint
a magspinek és a vezetési elektronok spinjei közti hiperfinom kölcsönhatásból
származó hosszútávú (oszcilláló) kicserélõdési potenciál adja
a Hamilton-operátor domináns részét.
szöggel elforduló spirál.
Ez a modell helyesen írja le egyes ritkaföldfémek és átmenetifém-vegyületek
alapállapotát, amelyekben ismereteink szerint
a magspinek és a vezetési elektronok spinjei közti hiperfinom kölcsönhatásból
származó hosszútávú (oszcilláló) kicserélõdési potenciál adja
a Hamilton-operátor domináns részét.
Ennek értelmében írjuk a tökéletes spirál (kristálytér-effektusok, stb.
elhanyagolásával egyszerûsített) Hamilton-operátorát a következõ formába:
ahol 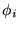 az
az
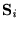 spin és az x-tengely által bezárt szög,
Jij pedig az
spin és az x-tengely által bezárt szög,
Jij pedig az
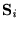 és
és
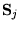 spinek kicserélõdési
csatolását írja le (Jii=0,
Jij=Jji).
spinek kicserélõdési
csatolását írja le (Jii=0,
Jij=Jji).
Ezek után képzeljük el, hogy egy bizonyos pontba egy az elõzõektõl kissé
eltérõ
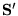 spinû mágneses szennyezõ kerül.
spinû mágneses szennyezõ kerül.
Gondoljuk át a szennyezõdés fizikai következményeit, majd számítsuk ki
az újonnan kapott spirálnak az eredeti ideálishoz képesti
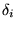 torzulási szögét az összes i pontra nézve! Diszkutáljuk a
kapott eredményeket!
torzulási szögét az összes i pontra nézve! Diszkutáljuk a
kapott eredményeket!
(Magyar Péter)
- 31.
- Csatlakoztassunk egy hõtartályhoz egy olyan, m tömegû
részecskékbõl álló
Fermi-gázt, melynek minden módusa
azonos energiájú! Bármely két részecske között
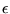 energiájú
kölcsönhátás lép fel. Vizsgáljuk meg a rendszer termodinamikáját!
energiájú
kölcsönhátás lép fel. Vizsgáljuk meg a rendszer termodinamikáját!
(Borsányi Szabolcs)
- 32.
- Ideális Bose-gázt tart fogva a
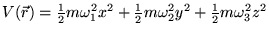 harmonikus
csapdapotenciál.
Határozzuk meg a Bose-kondenzáció kritikus hõmérsékletét és
a kondenzátum részecskeszámának hõmérsékletfüggését!
harmonikus
csapdapotenciál.
Határozzuk meg a Bose-kondenzáció kritikus hõmérsékletét és
a kondenzátum részecskeszámának hõmérsékletfüggését!
(Bene Gyula)
- 33.
- Sok esetben fontos az elektronikában (alakatrészekben, eszközökben)
felhasználásra kerülõ anyagok elõzetes vizsgálata -- pl. nagyon alacsony,
akár 1 K körüli hõmérsékleteken is. Az ideális esetekben az apró mintán
keresztül az áram kontaktustól kontaktusig egyenletesen folyik, de gyártás
tökéletlensége, valamint az elkerülhetetlen inhomogenitások és szennyezõk
miatt egy ún. "disordered", azaz véletlenszerû, szimmetria nélküli
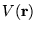 szórópotenciál is megjelenik (a kristály szabályos,
rácsperiodikus, az m* effektív tömegen keresztül figyelembe vett
szórópotenciál is megjelenik (a kristály szabályos,
rácsperiodikus, az m* effektív tömegen keresztül figyelembe vett
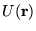 potenciálja mellett), amely a teljes áram egy részét
szabálytalan alakú és kiterjedésû csatornákba szorítja, míg más helyeken
szinte alig halad át töltéshordozó.
Ennek eredményeképpen a felszín alatt, valahol a minta belsejében térben
korlátos szûk tartományokban extra disszipáció lép fel. Ezeknek az általában
néhányszor tíz
potenciálja mellett), amely a teljes áram egy részét
szabálytalan alakú és kiterjedésû csatornákba szorítja, míg más helyeken
szinte alig halad át töltéshordozó.
Ennek eredményeképpen a felszín alatt, valahol a minta belsejében térben
korlátos szûk tartományokban extra disszipáció lép fel. Ezeknek az általában
néhányszor tíz 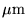 kiterjedésû disszipatív "szigeteknek" a
megfigyelése
technológiai szempontból igen fontos, ehhez pedig rendkivül érzékeny
hõmérsékletmérésre van szûkség.
kiterjedésû disszipatív "szigeteknek" a
megfigyelése
technológiai szempontból igen fontos, ehhez pedig rendkivül érzékeny
hõmérsékletmérésre van szûkség.
Na most jön a képzelet birodalma. Tegyük fel, hogy a laborunk csóró
(...)
és a hõmérõink egytõl egyig mind elavultak. Van azonban egy jó lézerünk, a
csapból pedig ömlik a szuperfolyékony 4He. Ettõl szárnyakat kapunk, és
elkezdünk gondolkodni... a szuperfolyékony 4He egy csomó érdekes
tulajdonságot, jelenséget mutat ... ha ezek közül néhányat ki tudnánk
használni
felületi termográfiára, más szóval át tudnánk váltani a
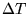 -t
-t 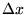 -re ...
(Tegyünk így, becsszóra, lehet ...)
-re ...
(Tegyünk így, becsszóra, lehet ...)
a) Találjuk meg az alkalmas kísérleti elrendezést, magyarázzuk meg a
mérés elvét, és végezzünk néhány egyszerû konkrét számítást is!
b) Mi a (kitalált) módszer érzékenyége? Szükség esetén használjunk
néhány realisztikus számadatot! A lézer mérési pontosságát (felbontás)
vegyük kb. 1 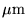 -nek!
-nek!
(Magyar Péter)
- 34.
- Különös lények élnek egy távoli kétdimenziós bolygón.
Mindegyikük szívében
egy kis antenna található, mely egy egységnyi hosszúságú
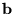 vektorral adható meg, ha a lény ébren van - alvó lény
esetén pedig
vektorral adható meg, ha a lény ébren van - alvó lény
esetén pedig 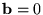 .
Az ellentétes irányú
.
Az ellentétes irányú 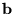 vektorral rendelkezõ egyedek nagy vonzalmat (a mi fogalmaink szerint
szerelmet) mutatnak egymás iránt. Egy napon a bájos Antennova egy
nagy kerek tó közepén levõ aprócska szigetre csónakázott,
hogy virágot
szedjen. Sajnos nem volt elég gondos, és csónakját elsodorta a
víz.
Szegény szomorúan és tétlenül üldögélt a szigeten, mivel
nem tudott
úszni. Abban reménykedett, hogy talán valaki arra jár, és segít
neki. Már
elég késõre járt, mikor megjelent a hõs Antennovics, aki
melleseleg igen
forrón imádta a bájos Antennovát. Mindkettõjük szíve
megdobbant - ó minõ jelenet! Kár, hogy nem látta senki -
hiszen a bolygón mindeki más mélyen aludt.
vektorral rendelkezõ egyedek nagy vonzalmat (a mi fogalmaink szerint
szerelmet) mutatnak egymás iránt. Egy napon a bájos Antennova egy
nagy kerek tó közepén levõ aprócska szigetre csónakázott,
hogy virágot
szedjen. Sajnos nem volt elég gondos, és csónakját elsodorta a
víz.
Szegény szomorúan és tétlenül üldögélt a szigeten, mivel
nem tudott
úszni. Abban reménykedett, hogy talán valaki arra jár, és segít
neki. Már
elég késõre járt, mikor megjelent a hõs Antennovics, aki
melleseleg igen
forrón imádta a bájos Antennovát. Mindkettõjük szíve
megdobbant - ó minõ jelenet! Kár, hogy nem látta senki -
hiszen a bolygón mindeki más mélyen aludt.
A hõs
Antennovics nem habozott, és tüstént megpróbált segíteni a
bajba jutott
kedvesének. A baj csak az volt, hogy õ sem tudott úszni. Igen
bosszankodott
emiatt, még a fejét is elvesztette. Le-föl (pontosabban körbe-körbe)
szaladgált a kerek tó mentén. E véletlenszerû "termikus tánc"
csak a kettejük közti kölcsönhatástól és a külsõ
hõmérséklettõl függ.
A bolygó különös lakóinak
életét már régóta tanulmányozták a kutatók, bevonva
néhány fizikus hallgatót
is. Az eddigi kutatási eredmények szerint a párok közötti
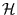 kölcsönhatást az alábbi egyszerû alakban adhatjuk meg
kölcsönhatást az alábbi egyszerû alakban adhatjuk meg
ahol 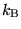 a Boltzmann állandó, T a hõmérséklet,
a Boltzmann állandó, T a hõmérséklet,
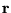 a két lényt összekötõ vektor, míg
a két lényt összekötõ vektor, míg 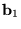 ,
,
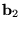 a megfelelõ antennavektoruk és K a csatolási állandó.
A kutatócsoport fizikus hallgatói a következõ ötlettel
próbálták meghatározni
az eddig még ismeretlen K csatolási állandót. Nagyszámú
fényképfelvételt készítettek a hõs Antennovics helyzetérõl. A
felvételekbõl meghatározták a párt összekötõ
a megfelelõ antennavektoruk és K a csatolási állandó.
A kutatócsoport fizikus hallgatói a következõ ötlettel
próbálták meghatározni
az eddig még ismeretlen K csatolási állandót. Nagyszámú
fényképfelvételt készítettek a hõs Antennovics helyzetérõl. A
felvételekbõl meghatározták a párt összekötõ 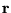 vektort, majd
elkészítették az <ri rj> átlagot (itt ri az
vektort, majd
elkészítették az <ri rj> átlagot (itt ri az 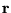 vektor
i-dik komponense). Feltették, hogy elegendõ felvétel áll
rendelkezésükre,
hogy a fenti átlagot a termodinamikai átlaggal helyettesítsék. Az
egymás iránti - szemmel láthatóan - erõs vonzalom alapján azt is
feltették, hogy a szerelmes pár antennavektorai ellentétes irányúak
(az eddigi kutatások tanusága szerint ezt joggal gondolhatták).
vektor
i-dik komponense). Feltették, hogy elegendõ felvétel áll
rendelkezésükre,
hogy a fenti átlagot a termodinamikai átlaggal helyettesítsék. Az
egymás iránti - szemmel láthatóan - erõs vonzalom alapján azt is
feltették, hogy a szerelmes pár antennavektorai ellentétes irányúak
(az eddigi kutatások tanusága szerint ezt joggal gondolhatták).
A számításaik során gondok merültek fel, ezért az Ortvay
versenyzõk segítségét
kérik. Hogyan lehet a fentiek alapján meghatározni a K csatolási
állandót?
Meg lehet-e határozni e kedves pár antennavektorait?
(Cserti József)
- 35.
- A Roland-hágó a francia Pireneusok egyik legmeglepõbb
látványa: egy
hatalmas sziklafalból jókora darab hiányzik
(lásd az ábrát.
A legenda szerint a hõs
Roland itt csatázott a mórokkal, és közülük sok százat
pazar kardjának
élére hányt, ám egy idõ után érezte, hogy ereje kezdi elhagyni.
Nem is az
bosszantotta leginkább, hogy meg kell halnia, hiszen hõs volt
(lásd fentebb),
hanem az, hogy kardja az ellenség kezére juthat. Így hát
összeszedte utolsó
erejét, hogy kardját egy nagy sziklán kicsorbítsa --
és akkorát talált
odasózni, hogy a francia Pireneusok csorbultak ki.
Szamítsuk ki, milyen fizikai következményekkel jár a
fenti interpretáció!
(Piróth Attila)
 end{document}
end{document}



Next: About this document ...
Jozsef Cserti
1998-10-30
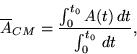
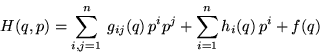
![]() általános koordinátatranszformáció során, ha azt akarjuk,
hogy
általános koordinátatranszformáció során, ha azt akarjuk,
hogy ![]() kovariánsan transzformálódjon?
Alkalmazzuk a fenti eredményeket a kétdimenziós harmonikus
oszcillátorra Descartes- és polárkoordináta-rendszer-beli
kvantálás esetén!
kovariánsan transzformálódjon?
Alkalmazzuk a fenti eredményeket a kétdimenziós harmonikus
oszcillátorra Descartes- és polárkoordináta-rendszer-beli
kvantálás esetén!
![]() spinû mágneses szennyezõ kerül.
spinû mágneses szennyezõ kerül.
![]() torzulási szögét az összes i pontra nézve! Diszkutáljuk a
kapott eredményeket!
torzulási szögét az összes i pontra nézve! Diszkutáljuk a
kapott eredményeket!
![]() -t
-t ![]() -re ...
(Tegyünk így, becsszóra, lehet ...)
-re ...
(Tegyünk így, becsszóra, lehet ...)
![]() -nek!
-nek!
![]() kölcsönhatást az alábbi egyszerû alakban adhatjuk meg
kölcsönhatást az alábbi egyszerû alakban adhatjuk meg