


Next: About this document ...
THE 29th
- FOR THE FIRST TIME INTERNATIONAL -
RUDOLF ORTVAY
PROBLEM SOLVING CONTEST IN PHYSICS
1998
PROBLEMS
The Physics Students' Association of Eötvös University, Budapest and the
Hungarian Association of Physics Students proudly announce the traditional,
29th -- and for the first time international --
Rudolf Ortvay Problem Solving Contest in Physics,
from October 30, 1998 through November 9, 1998.
The Ortvay Contest is an old tradition at Eötvös University. Many former
contestants have become famous scientists and university professors, and they
had showed their first marks of genius fighting with Ortvay-problems some
years ago.
For the first -- hopefully not last -- time, the contest is announced
internationally in 1998, as -- owing to the preliminary propaganda -- letters
showing interest have arrived from more than 20 countries. Thus, we wish to
give a good occasion for students of different universities and countries to
cross their swords of knowledge, ingenuity, problem-solving skills and physical
insight into problems that are far beyond routine-level. Although prizes are
given only to individual participants, such an extensive contest also means a
rivalry among the universities guiding the intellectual development of the
contestants.
Every university student can participate in the Ortvay Contest. PhD students
compete in a separate category. The contest is for individuals; solutions sent
by groups of students are not accepted. The name, the university, the major,
and the university year should be given. Pseudonyms and passwords cannot be
used: each contestant has to use his/her own name.
The problems can be downloaded from the webpage of the Ortvay Contest
(http://ludens.elte.hu/ortvay)
in Hungarian and English languages, in html and LATEX formats, from 12
o'clock (Central European Time), Friday, October 30, 1998. On preliminary
requests sent to dgy@ludens.elte.hu, the problems will be sent
via email, too.
The problems will be distributed by local organizers at many foreign
universities, too.
Despite all the efforts of the organizers, it may happen that some
unclear points or spelling mistakes stay in the text. Therefore it is very
useful to visit the webpage of the contest every so often, as the corrections
and/or modifications will appear there.
The problems of the contest come from different branches of theoretical
physics as well as applicational fields of physics. 30 to 35 problems are
assigned each year. These are of different levels of difficulty, and every
contestant can find problems appropriate to their university level. Each
contestant can send solutions for 10 problems. For the solution of each
problem 100 points can be given. Each problem should be presented on (a)
separate A4, or letter-sized sheet(s). The contestants are kindly asked to
use only one side of each sheet. Solutions written by pencil or written on
thin copy-paper will not be accepted as these cannot be faxed to the referees.
Any kind of reference may be consulted; textbooks and articles of journals
can be cited. Computer programs appended to the solutions should be accompanied
by detailed descriptions (what computer language it was written in, how to
start the program, which parameters can be set, what notations are used, how
to interpret the output figures and graphs, etc.) They can be enclosed on
floppy disks, or sent via email to the address given below.
Solutions can be sent by mail, fax, or email (in LATEX
format -- or, if it contains no formulae,
in normal electronic mail):
Postal Address: Fizikus Diákkör, Dávid Gyula,
ELTE TTK Hallgatói Iroda, Gólyavár,
H-1088 Budapest, Múzeum krt. 6-8.
Fax: Dávid Gyula, 36-1-2662556
Email: dgy@ludens.elte.hu
Deadline for sending the solutions: 12 o'clock (CET), 9 November, 1998.
The contest will be evaluated separately for each university year, according
to the total number of points. The referees reserve the right to withhold,
to multiply
or to share some prizes. Beyond the money prizes given for the first,
second, and third places, honourable mentions and special prizes for the
oustanding solutions of individual problems can be awarded. This is why it
is worthwhile sending even one or two solutions.
The traditional sponsors of the contest are the Students' Foundation of the
Faculty of Sciences of Eötvös University, and the Roland Eötvös
Physical Society. Furthermore, our regular patron, Lajos Diósi offered a
special prize of HUF 20000. The best contestant of József Attila University,
Szeged will be awarded HUF 5000 by Pro Patria Students' Foundation.
Their help is highly acknowledged -- and warmly welcome in the future.
The announcement of the results will take place on 3 December. The detailed
result will be available on the webpage of the contest thereafter. Diplomas
and money prizes will be sent by mail.
We plan to publish the assigned problems and their solutions in English
language -- to which the contribution of the most successful solvers is
kindly asked. The volume is planned to be distributed all over the world with
the help of the International Association of Physics Students, as well as the
contestant themselves. We hope this will help in making the contest even more
international.
Wishing a successful contest, rich and useful problem-solving to all our
contestants,
on behalf of the organizing committee,
Dávid Gyula
Physics Students' Association of Eötvös University
dgy@ludens.elte.hu
- 1.
- Wine is fermented from grapes. During the process, heat is produced.
a) What temperature does a 500-litre barrel reach for different sorts of wine?
b) What parameters play the most important roles in determining this
temperature?
c) Fermenting bacteria die beyond a certain temperature. What is the maximal
size of a barrel in which must is continually fermenting everywhere? How does
this size depend on the external temperature?
(Anna Horváth)
- 2.
- If we look between two parallel mirrors, we can see an apparently
infinite sequence of images. Because of the finite size of the mirror,
however, only a finite number of images can be seen.
a) How does the number of images depend on the size and the shape of the
mirrors?
b) Study various methods that can be used to observe the images in the
parallel mirrors. (Discuss only experimentally feasible methods.)
(Anna Horváth)
- 3.
- On winter mornings the windscreens of the cars are often frozen only on the
Eastern side. Why? Give a quantitative explanation.
(Gyula Bene)
- 4.
- One end of a broomstick of length l is fixed to a pivot located at a distance
a < l from a vertical wall. The other end of the broomstick is leaning
against the wall. Move the broomstick a bit to one side; due to friction it
will stay in equilibrium up to a certain point. At what critical angle will the
broomstick slid?
Describe the motion of the broomstick, if it is set vertically and is then
given an initial impulse.
(Péter Gnädig)
- 5.
- A tower is built from bricks of given size with elastic constants
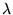 and
and 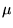 .
What is the maximal height of a stable tower?
.
What is the maximal height of a stable tower?
(Géza Tichy)
- 6.
- In elasticity one derives from the displacement vector ui the
strain tensor
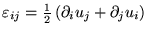 for which the following compatibility condition holds:
for which the following compatibility condition holds:
where
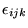 is the permutation symbol, or Levi-Civita symbol.
is the permutation symbol, or Levi-Civita symbol.
How can we construct the displacement vector from the strain tensor?
(Géza Tichy)
- 7.
- The accuracy of hearing is mechanically determined by the shape of the
tympanic membrane. Explain why tympanic membranes which have regular shapes
(circle, ellipse) are superior (from the
viewpoint of accurate hearing) to those with irregular ones.
(The accuracy of hearing is understood as the extent to which one can
distinguish two sounds with almost equal frequencies.)
(Anna Horváth)
- 8.
- Human blood cannot transport a sufficient amount of oxygen in
physically dissolved state. This is the reason why we have red blood cells
(RBC) that can make this transfer. But what ``price'' do we pay for this? In
other words, how much excess energy is spent on RBC transport by Tom, Dick,
and Harry on a normal day, compared to the hypothetical case when
RBC's are not needed? (The total volume of the blood is the same in the
two cases.)
One should think over the following: RBC's have to get across the capillaries
(which are narrower than the diameter of the RBC's); blood flows more rapidly
than RBC's; the density of RBC's is different from that of blood, and so extra
energy is necessary to move the RBC's (due to gravity).
(György Nagy)
- 9.
- We got caught in the rain on an outing and we found shelter under the
eaves of a building, from where we were watching the hopeless weather and
the raindrops that were gathering on the bottom of the eaves, and, having
grown large enough, they started to move towards the drain. Investigate the
instability that occurs during the formation of the drops. Determine the
position of the drop as a function of time until it leaves the eaves. Can a
drop catch up with another?
(János Török)
- 10.
- A pipette is held vertically with its opening pointing downwards.
Liquid is flowing out of the pipette with constant velocity.
What are the conditions of drop formation at the opening of the pipette?
If these conditions are fulfilled, describe the form of the drops
as a function of time!
(Farkas Zénó)
- 11.
- Pouring dry sand into a vertical (glass) tube one can observe density
waves moving upwards in the material flowing downwards. (It's worth
trying!)
The phenomenon is similar to the propagation of traffic jams. What is its
explanation? What does the velocity of the waves depend on?
(János Kertész)
- 12.
- In L. Niven's scientific novel, Ring World -- apart from other
fascinating
technical ideas -- the following object is mentioned. A very large number of
identical, equidistant artificial satellites are set in motion on a circular
orbit about a star. The satellites are connected by unstretchable chains
along the circle, and, by means of rockets, the whole system is spinned to an
angular velocity that is much larger than the orbital angular velocity
corresponding to the radius in question. (What this is good for? Read the
book.) Investigate the stability of the system, and determine the dispersion
relation of the waves propagating around the circle, in the case of
perturbations that are longitudinal, radial, and perpendicular to the orbital
plane.
(Gyula Dávid)
- 13.
- Two identical insulating disks are given identical amounts of positive charge.
Move the two disks towards each other. What force has to be applied? Sketch
the electric field that is present between the two disks.
(Gyula Radnai - Péter Gnädig)
- 14.
- Into what shape should we fold a given insulated copper wire to get the
largest possible inductance? Consider a homogeneous copper wire whose length
is
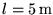 ,
whose cross section is a circle with radius
,
whose cross section is a circle with radius
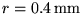 ,
and the insulating layer covering it is
,
and the insulating layer covering it is
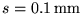 thick.
What maximal inductance can be obtained by folding this wire? (There are
no ferromagnetic bodies around.)
thick.
What maximal inductance can be obtained by folding this wire? (There are
no ferromagnetic bodies around.)
As a warming-up excercise, determine the ratio of the inductances of the
circular and square-shaped loops folded from this wire.
(Gyula Radnai)
- 15.
- Suppose the components of the electromagnetic four-potential (Ai) and
the four-current-density (ji) can assume not only real values but also
a) complex; b) quaternion values. Construct the Lorentz-invariant
action, and derive the field equations. Formulate these hyper-Maxwell equations
in terms of partial differential equation systems of real three-vectors, and
find some interesting solutions. (E.g. plane wave, monopole, Green's function,
etc.) What new symmetries does this theory have that are absent in the ordinary
one? What are the corresponding conservation laws? What real phenomena could
be modelled by this (hyper)complex electrodynamics?
Add a mass term to the action, and investigate the consequences.
(Gyula Dávid)
- 16.
- The first (and last) Formula-42 photon rocket race was orgainzed in the
year 2442, and took place in the breathtaking Minkowski space, next door to
the outermost Spiral Arm of the Milky Way, in the great void. The race had to
take place here, as according to the rather strict regulations of the Space-Way
Code, under no circumstances can two photon rockets be closer to each other
than 1000 kilometres, so the space is really needed. The rockets taking part in
Formula-42 races have the shape of an ellipsoid of revolution whose length is 1
kilometre, and whose diameter is 10 metres. (This huge vehicle is equipped
with enough fuel for 42 years' of incessant use. The fuel is anameson, which
can be utilezed with a higher efficiency than antimatter.)
The position-indicating lights mounted on the bow and the stern of each rocket,
emit a green and a red light signal every second, according to the Navigation
Regulations. The main organizer, Bernie Ecclestar took some extra measures for
the sake of a fair contest: the same engine has to be mounted on each rocket.
This `Feel-at-Home' engine provides the spaceship with a proper acceleration
g -- so the pilots feel as if they were sitting at home in the amusement
arcade. Due to unfortunate technical problems, 40 of the 42 contestants had
to retire. The race of the two remaining rockets was a bit boring: floating at
an approximate distance of 100000 kilometres from each other they shot out
perpendicularly to the start line, and then -- having the same
structure -- flying in parallel lines with identical accelerations and keeping
the perfect symmetry the race was tied.
Needless to say, the spectartors could not see too much of the hot-rod rockets.
However, by stroke of good fortune, some competing TV channels placed cameras
and robot reporters aboard the rockets. The automatic cameras were focused on
the other rocket -- what else was there to see? -- and the robot reporters
were
following the slightest turns of the frame of the cameras in trance, trying to
figure out the standings from this (and the apparent angular diameter and the
orientation of the other rocket, of course). Thus the spectators could enjoy a
fairly exciting virtual race on the TV screens.
In the second heat the second rocket -- in a highly gentlepersonlike
manner -- gave a start of 100000 kilometres to the first one, and so they were
running along the same perfectly, straight cosmic track.
The robot reporters were following this rather weird TV-race in an entire rave
throughout the contest.
Calculate/describe/draw what could be seen on the screens during the first
race, and during the second one from the front and the rear rocket. How
did the distance, the direction, the orientation, the angular diameter, the
signal colour and the brightness of the other rocket change in time?
And finally: how, when, and why did the race come to an end?
(Gyula Dávid)
- 17.
- The pilots of the two rockets competing in the Formula-42 race decided
to test Einstein's famous paradox about the contraction of (kilo)metre rods.
Therefore, they connect the two spaceships (that float behind one another)
by a 1-kilometre rod. In a given instant of time they both start the engine of
their rockets, and they turn them off 1 second later. (The direction of the
acceleration is parallel to that of the rod.) The pilots had got their
A pulses in the scientific kindergarten, so they know that according to the
theory of relativity there is no such thing as a rigid body, and that due to
the forces exerted on the two ends of the rod, longitudinal waves are formed
in the rod. In order to take this into account they tested the elastic
properties of the rod, and measured the coefficients in the telegraph
equation of the longitudinal waves. Therefore they hope that the waves would
gradually relax and the rod would get into an equilibrium state in the new
inertial frame of the two rockets. Follow the propagation of the waves in
the accelerating phase and after the engines are turned off. Determine the
length of the rod in the final state. What would professor Einstein say?
(Gyula Dávid)
- 18.
- One of the rockets of the Formula-42 race (filled up with an even more
abundant, practically inexhaustible fuel supply) makes a test drive in the
even more breathtaking Riemann space. Floating by the edge of the Solar
System, they aim at one of the dark, galaxy-free points of the Celestial
sphere, and hey, burn up the road! On the way they are watching the interesting
space-scapes of the Universe. What can the cosmonauts see? How does the
brightness and the distribution of the galaxies, and the angluar distribution
and the temperature of the cosmic background radiation depend on the
angle? Calculate these data referred to the proper time of the spaceship, and
plot them. Give the answer in the case of Einstein's static universe, as well
as for expanding universes of Friedmanian open and closed types, and Euclidean
type, too. What will happen to the spaceship in the distant future?
(Gyula Dávid)
- 19.
- Some people say that there is no gravitational interaction between
cosmic objects in 2+1-dimensional general relativity. (Why, is there in the
3+1 dimensional theory?) If the statement is true, what the heck is the
2+1-dimensional theory all about? And if it is not true, why is it true,
anyway?
(Gyula Dávid)
- 20.
- Determine the eigenvalue spectrum of the following Hamiltonian:
(József Cserti)
- 21.
- Besides spin, it is perhaps the uncertainty relation
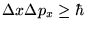 ,
etc., that is most often quoted as
`a purely quantum mechnical (QM) phenomenon having no
classical counterpart'. For those with a rebel mind this may sound
a bit of mistification, so one may feel tempted to lead an attact against
this stronghold of axiomatic QM. Perhaps things are not so bad after all,
and
our common sense of quantum-to-classical correspondence is not violated.
The uncertainty principle involves the calculation of the standard
deviation of physical quantities A around their mean values:
,
etc., that is most often quoted as
`a purely quantum mechnical (QM) phenomenon having no
classical counterpart'. For those with a rebel mind this may sound
a bit of mistification, so one may feel tempted to lead an attact against
this stronghold of axiomatic QM. Perhaps things are not so bad after all,
and
our common sense of quantum-to-classical correspondence is not violated.
The uncertainty principle involves the calculation of the standard
deviation of physical quantities A around their mean values:
In QM, the average in above equation is (for simplicity in 1D):
where 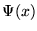 is the normalized wave function of the system. In
classical mechanics (CM) it is not so evident what to take as average, but
without a better clue, as a working hypothesis one might define the
avarage of A as a time average:
is the normalized wave function of the system. In
classical mechanics (CM) it is not so evident what to take as average, but
without a better clue, as a working hypothesis one might define the
avarage of A as a time average:
To check whether or not this somewhat weird choice is viable, consider
a specific system. The similarity between CM and QM motions (the Kepler
problem and the hydrogen atom, respectively) in the attractive central
potential
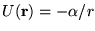 was noted a long time ago; besides,
orbitals, wave functions, and energies are well-known.
was noted a long time ago; besides,
orbitals, wave functions, and energies are well-known.
a) Choosing appropriate coordinate systems calculate
the uncertainties of a suitable coordinate and the corresponding momentum.
Use the above definitions (our a better one if you have...).
Is there any connection between the CM and QM results?
b) Is there then an uncertainty principle in the classical limit?
What is the meaning of the definition of classical average in this context?
(Péter Magyar)
- 22.
- A mechanical system is defined by the following Hamiltonian:
where
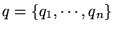 is the short-hand notation for the collection of the configuration space
coordinates.
is the short-hand notation for the collection of the configuration space
coordinates.
Quantize the system according to the Schrödinger prescription:
Try to fix the factor-ordering problem by demanding that the Hamiltonian
be self-adjoint for the inner product
Find the transformation law for the wave function under the (generic)
coordinate transformation
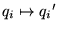 ,
such that
,
such that
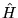 transforms covariantly.
Apply the obtained results for a two-dimensional harmonic oscillator
quantized in Descartes and polar coordinate systems.
transforms covariantly.
Apply the obtained results for a two-dimensional harmonic oscillator
quantized in Descartes and polar coordinate systems.
(Zoltán Bajnok )
- 23.
- Electrons are fermions, and so, according to the Pauli exclusion
principle, they cannot be in identical states. However, electrons form pairs
in superconductors (the Cooper pairs), which are bosons, and so they can be
in identical states. Is there a contradiction? Justify your answer with
detailed calculations.
(Gyula Bene)
- 24.
- Investigate whether coherent states can be defined in the case of a
plane rotator. Which properties of the coherent states of a harmonic
oscillators can be taken over, and which ones have to be abandoned? What is
the connection between the new coherent states and the shifting operators?
(Szabolcs Borsányi)
- 25.
- Two bosons move in a one-dimensional, infinitely deep square potential
well (i.e. V(x) = 0, if
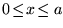 ,
and
,
and
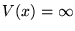 otherwise). They collide with each other as rigid bodies. Determine the
energy eigenvalues and the energy eigenstates.
otherwise). They collide with each other as rigid bodies. Determine the
energy eigenvalues and the energy eigenstates.
(Gyula Bene)
- 26.
- The low-lying excitations of trapped Bose-condensed gases are
given by the solutions of the following eigenvalue problem:
In real experiments the potential
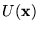 is chosen as
is chosen as
where 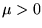 is the chemical potential, m is the mass
of the atoms,
is the chemical potential, m is the mass
of the atoms, 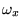 ,
,
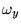 ,
,
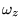 are the characteristic
frequencies of the trap, and
are the characteristic
frequencies of the trap, and
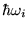 are the excitation energies.
Find other operators (built up from the coordinates x, y, z
and from derivatives with respect to these coordinates) that commute
with
are the excitation energies.
Find other operators (built up from the coordinates x, y, z
and from derivatives with respect to these coordinates) that commute
with 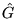 .
.
(András Csordás)
- 27.
- Can local thermal equilibrium be maintained in a monoatomic,
perfect gas without collisions, just by the free streaming of the particles?
Surprisingly, the answer to theis question is positive. Why? Determine the
time evolution of the phase-space distribution function
f(t, x,
p) as well as the local density, temperature and velocity fields
n(t, x),
T(t, x), and
x(t, x), respectively,
for such a clooisionless, locally thermalized gas.
(Tamás Csörgõ)
- 28.
- Thermions -- as it is well-known from the 1996 Ortvay Contest -- are
hypothetical particles that assume the temperature of the environment very
quickly. According to Boltzmann, E = kT, while Einstein says E = mc2; all
in all the mass of a thermion is always proportional to the temperature of the
local environment. This needs no proof, just a bit of faith.
Thermions come in three species. Hotons love hot places, therefore
they are acted upon by a force that is proportional to the temperature
gradient. On the other hand, shiverons love cold places, thus the force
acting upon them is the opposite of the previous one (with equal magnitude).
Temperons love temperate places, therefore the force acting upon them is
proportional to the vector product of their velocity vector and the
temperature gradient. (Further sub-species can be defined if necessary for
the calculations).
(It is advisable to denote the constant parameters of
velocity dimension by c).
Investigate the thermodynamical characteristics of a perfect gas that
consists of thermions. First assume that the gas is homogeneous, i.e. only one
of the three species of thermions is present. Derive the equations of state.
Consider a tube that is separated into two parts by a piston. What happens, if
different species of thermions are put in the two parts? (Consider the cases of
heat-conducting and heat-insulating pistons.)
What happens, if the mixing of two species is allowed?
Investigate the mechanical and thermodynamical stability of the system.
(Gyula Dávid)
- 29.
- The mean-field approximation reduces the solution of the Ising model to a
single-spin problem: a selected spin is treated exactly and the
interacting neighbours are replaced by the averages. The fact that the
Ising chain can be solved exactly suggests an extension of the
approximation: the model is considered as a system of interacting chains,
a selected chain is treated exactly and the spins on the neighbouring
chains are replaced by the averages.
Compare the two approximations by calculating the transition temperature
of an Ising model on a simple cubic lattice, assuming different exchange
couplings in the xy plane and in the z direction. The energy of the
model is given by
where i,j,k are integer coordinates of the lattice points and
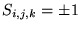 .
.
(László Sasvári)
- 30.
- Consdider a one-dimensional chain along which equal spins
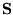 (
(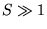 )
are located at regular distances
a from each other. The spins (due to the atomic symmetries that manifest
themselves in the shape of the electron cloud) can only rotate in the
x-y plane, which is perpendicular to the axis of the chain
(z-axis),
and in equilibrium (at T=0, with no external field) they form a
spiral whose turn angle between two adjacent sites is
)
are located at regular distances
a from each other. The spins (due to the atomic symmetries that manifest
themselves in the shape of the electron cloud) can only rotate in the
x-y plane, which is perpendicular to the axis of the chain
(z-axis),
and in equilibrium (at T=0, with no external field) they form a
spiral whose turn angle between two adjacent sites is 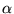 .
This model correctly describes the ground state of certain
rare earth metals and transition metal compounds, where the long range
(oscillating) exchange potential arising from hyperfine interaction
between nuclear spins and conduction electron spins is the dominant part
of the Hamiltonian.
.
This model correctly describes the ground state of certain
rare earth metals and transition metal compounds, where the long range
(oscillating) exchange potential arising from hyperfine interaction
between nuclear spins and conduction electron spins is the dominant part
of the Hamiltonian.
In this spirit, we may write the Hamiltonian (simplified by neglecting
crystal field effects, etc.) of the perfect spiral as
where 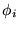 is the angle formed by
is the angle formed by
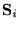 and the
x-axis, whil Jij characterizes the exchange coupling between spins
and the
x-axis, whil Jij characterizes the exchange coupling between spins
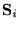 and
and
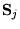 with Jii=0,
Jij=Jji.
with Jii=0,
Jij=Jji.
Now imagine that at one site a magnetic impurity with a slightly different
spin
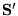 is introduced.
is introduced.
Consider the physical consequences of the effect of the impurity, and find
the distortion angle 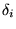 of the new spiral with respect to the turn
angle of the ideal one at all sites i.
Discuss the results.
of the new spiral with respect to the turn
angle of the ideal one at all sites i.
Discuss the results.
(Péter Magyar)
- 31.
- Connect a Fermi gas -- all modes of which are of equal energy -- to a
heat reservoir. Between each pair of particles an interaction of energy
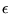 is present. Study the thermodynamics of the system.
is present. Study the thermodynamics of the system.
(Szabolcs Borsányi)
- 32.
- And ideal Bose gas is trapped in the harmonic potential
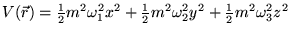 .
Determine the critical temperature of Bose
condensation, and the temperature dependence of the number of particles in
the condensate.
.
Determine the critical temperature of Bose
condensation, and the temperature dependence of the number of particles in
the condensate.
(Gyula Bene)
- 33.
- It is often important to test -- e.g. in experiments done at very low
temperatures, say around 1 K -- the quality of materilas used to
manufacture electronic devices. In the ideal case, current flows
uniformly from contact to contact in a small sample. However, due to
imperfect
fabrication and the presence of inevitable inhomogeneities and impurities,
a `disordered', asymmetric scattering potential
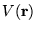 results (in addition to the regular crystal potential
results (in addition to the regular crystal potential
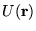 ,
which
is taken into account by the effective mass m*). This
causes excess current to flow through channels of irregular size, while
it leaves other regions almost empty.
This leads to extra dissipation in certain small pockets in the interior of
the sample somewhere beneath the surface.
The monitoring of these 'islands', whose typical diameter is of the
order of few times ten
,
which
is taken into account by the effective mass m*). This
causes excess current to flow through channels of irregular size, while
it leaves other regions almost empty.
This leads to extra dissipation in certain small pockets in the interior of
the sample somewhere beneath the surface.
The monitoring of these 'islands', whose typical diameter is of the
order of few times ten
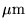 ,
is of great technological
interests and requires extremly precise temperature measurments.
,
is of great technological
interests and requires extremly precise temperature measurments.
Now comes fantasy.
Suppose that our lab is not very rich (...), and our thermometers are
pretty outdated. We have, though, a state-of-the-art laser at our disposal,
and plenty of superfluid 4He.
Inspired by this we start to think ... superfluid 4He has a number
of interesting properties ... now would it be possible to exploit
(some of) these and perform thermography on the surface of the sample,
thus converting 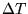 into
into 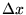 ?
(Take my guess: it is possible ...)
?
(Take my guess: it is possible ...)
a) Find the appropriate experimental setup, explain the underlying
principle, and make some explicit calculations.
b) What is the sensitivity of the method you have devised?
Use some appropriately chosen realistic numbers, if necessary.
Take the measuring precision of the laser to be cca. 1
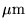 .
.
(Péter Magyar)
- 34.
- A remote, two-dimensional planet is inhabited by weird creatures. A small
antenna is present in the heart of each, which can be characterized by a unit
vector
b, when the weird creature is awake, and
b = 0 if it
is asleep.
Individuals characterized by antiparallel vectors
b
are greatly attracted by each other (love, according to terrestrial folklore).
One day the charming Antennowa took a boat and went to a small island in the
middle of a circular lake, to pick flowers. Alas, she was not careful enough,
and her boat was taken by the water. Poor thing, she was sitting sadly and idly
in the island, as she could not swim. She hoped somebody would come around and
help her. Time was passing, the night has arrived, when the celebrated hero,
Antennowich, -- who was madly in love with charming Antennowa -- appeared.
Both
hearts were throbbing -- imagine, what a scene it was! They would have deserved
some spectators -- but the whole planet was asleep.
Antennowich, the hero, did not waste his time, he immediately tried to give
help to his Luv. Alas, he knew nothing more about swimming than she did. Thus
he got very upset and lost his head. He was running up and down (or rather
around) the circular lake. This random ``thermal dance'' depends only on the
interaction between the couple and the temperature.
Researchers have long been studying the life of the weird inhabitants of the
planet. Several physics students are involved in this project. According to
studies completed up to now, the interaction
H
between two individuals can be given in the following simple form:
where kB is Boltzmann's constant, T is the temperature,
r is the
radius vector connecting the two individuals, 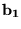 and
and 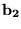 are
the antenna vectors, and K is the coupling constant. The physics students of
the staff tried to determine the coupling constant K as follows. They took a
large number of photos of the position of the great hero, Antennowich. From the
photos they determined the radius vector
r connecting the couple, and
then calculated the average
< ri rj > (where ri denotes the ith
component of
r.) They assumed that a sufficient number of photoes was
at hand, so they could regard the above average as the thermodynamical average.
On the basis of the (apparent) strong attraction between the two creatures
they also assumed that their antenna vectors are antiparallel (correctly,
according to previous studies).
are
the antenna vectors, and K is the coupling constant. The physics students of
the staff tried to determine the coupling constant K as follows. They took a
large number of photos of the position of the great hero, Antennowich. From the
photos they determined the radius vector
r connecting the couple, and
then calculated the average
< ri rj > (where ri denotes the ith
component of
r.) They assumed that a sufficient number of photoes was
at hand, so they could regard the above average as the thermodynamical average.
On the basis of the (apparent) strong attraction between the two creatures
they also assumed that their antenna vectors are antiparallel (correctly,
according to previous studies).
They came across serious difficulties in the calculations, so they asked for
the help of the Ortvay Contestants. How can the coupling constant K be
determined? Is it possible to determine the antenna vectors of the loving
couple?
(József Cserti)
- 35.
- `La brèche de Roland' is one of the most breathtaking sites in the
French Pyrenees: a huge part of a gigantic rockwall seems to have disappeared
(see the scanned photo at the website).
According to the myth, the heroic Roland was fighting here with the Moors,
and he chopped hundreds of them with his magnificient sword. However, after
some time he was getting exhausted. He knew he was to die. This was not
the thing that bugged him most, as he was a hero (see above), but rather
that his enemies would get hold of his sword. So, he took the last (giga)bits
of his strength to notch his sword on a huge rock -- and he happened to fetch
such a blow that the French Pyrenees got notched.
Calculate the physical consequences of the above interpretation.
(Attila Piróth)
 end{document}
end{document}



Next: About this document ...
Jozsef Cserti
1998-10-30
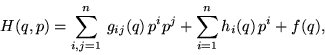
![]() is introduced.
is introduced.
![]() of the new spiral with respect to the turn
angle of the ideal one at all sites i.
Discuss the results.
of the new spiral with respect to the turn
angle of the ideal one at all sites i.
Discuss the results.
![]() into
into ![]() ?
(Take my guess: it is possible ...)
?
(Take my guess: it is possible ...)
![]() .
.